Introduction to Probability
6R
A probability tells
us the likelihood of an event happening.
Experimental Probability is based on the results of an experiment.
Experimental Probability =
Number of times an outcome
occurs
Number
of times the experiment is conducted
Theoretical Probability is found without conducting an experiment. It is the number of favourable outcomes as a fraction of the total number of possible outcomes.
Theoretical Probability = Number of favourable outcomes
Number of possible outcomes
All probabilities are
between 0 and 1. The probability is given as a decimal. It may be
written as a fraction or a percent as well.
![]()
P=0 P=0.25 P=0.5 P=0.75 P=1
Impossible Not likely half the time Quite likely Certain
If the probability is 0 you are saying it is virtually impossible for the event to happen, if you give as a decimal close to 1 you are saying there is a high certainty that it will occur.
For example, the sun coming up tomorrow P=1, and being hit by lightning P=0 or close to it.
P = 0.4 = 40% = 40/100 =4/10 = 2/5
To find the decimal, you divide the number of desired outcomes by the total number of outcomes.
View videos: http://www.onlinemathlearning.com/math-probabilty-1.html
Find the probability of a spinner:
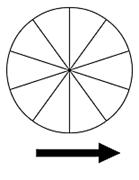 |
Number each section in the circle spinner from 0 to 9. 1. What is the probability of landing on the section labeled 2? P(2) Step one: How many sections are labeled with the number 2? _____ Step two: How many sections does the spinner have? ______ Make a fraction: Step one as the numerator and step two as the denominator. ______ The probability of P(2) = _______ 2. The probability of the spinner not landing on the section labeled 2 Would be P(not 2) = ________ |
Smarties Probability Work 6R Name_________________
1. Using a box of Smarties with these colours (O Y O BL BR PI BR Y BL R BR R Y O BR G Y G R O BR O PI G O BR PI BL R BR R Y O BR G Y G R O BR O PI O Y O BL BR PI BR Y) determine the probability of pulling out each colour out to the box as a fraction, a decimal, and a percent.
|
Colour |
Tally |
Fraction |
Decimal |
Percentage to 0.1 |
|
P(Yellow) = |
|
|
|
|
|
P( |
|
|
|
|
|
P(Red) = |
|
|
|
|
|
P(PUrple) = |
|
|
|
|
|
P(PInk) = |
|
|
|
|
|
P(BLue) = |
|
|
|
|
|
P(Green) = |
|
|
|
|
|
P(BRown) = |
|
|
|
|
2. Answer the following using a fraction, a decimal, and a percent.
a) What is the probability of finding a yellow in this box? P(yellow) =
b) What is the probability of not finding a yellow in this box? P(not yellow) =
c) What is the probability of finding a yellow or red in this box? P(yellow or red) =
d) What is the probability of not finding a red or orange in this box? P(not red or orange) =
|
3. 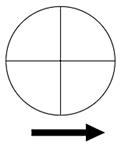 |
Colour the two top sections of this circle red, the bottom left green, and the bottom right yellow. Then answer the following questions. A fair game is one where all players are equally likely to win. When we express a probability as a percent, we often use the word chance to describe it. Give answers for a to e as a fraction, a decimal, and a percent - |
a) What is the probability of landing on red? P(red) =
b) What is the probability of landing on yellow? P(yellow) =
c) What is the probability of landing on green? P(green) =
d) What is the chance of landing on yellow or green? P(yellow or green) =
e) What is the chance of landing on yellow or red? P(yellow or red) =
f) What word you use to describe the probability of landing on red or green or yellow?
g) What word you use to describe the probability of landing on blue?
h) If Frank, Bill, and Ted were each given a colour, would this be a fair game?