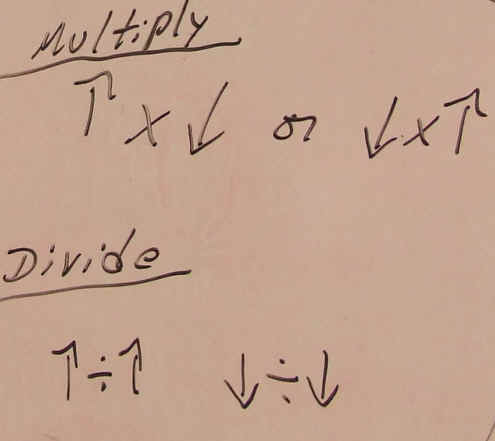Estimation by Doubling
Estimation: Creating "Friendly" Numbers
Doubling for Multiplication
Doubling for multiplication involves rounding and doubling or half-ing both
the top and bottom factors. This does not change the solution but can produce
"friendlier" products.
The first operation is to round the factors into usable numbers. Next
determine the factor to use to create an easy or a "1" number like 1,
10, 100, 1000, etc. to use. What ever you do to one factor do the opposite to
the other: if you multiple the top factor by 2 then divide the bottom factor by
2, this will keep the product the same.
Example:
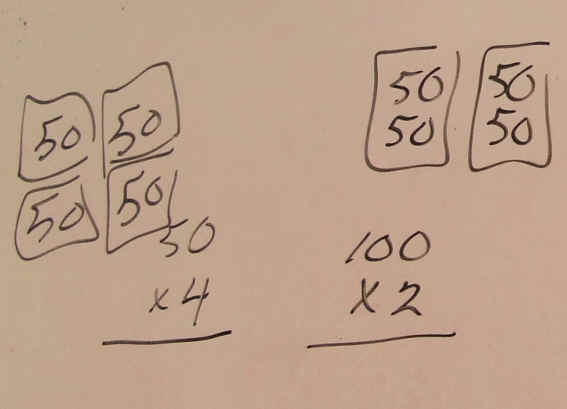 |
49
50 100
X 4 → X 4
→ X 2
200
The 49 was rounded to an even number 50 to make it easier to half or
double. When the top factor 50 was doubled to 100 the bottom factor 4 was
halved to 2. This kept the product 200 the same but provided
"nicer" numbers to use in the estimation.
|
Example:
24
25
50
100
X 64
→ X 64
→ X 32
→ X 16 This example
doubles and doubles again, or it could have
1600 been done in one less step using 4 instead of 2 and 2.
Example:
32
33
99
100 This example uses 3 to multiply and divide by, and rounds
X 27 → X
27 → X 9
→ X 9
at the beginning and at the end.
900
Doubling for Division
Doubling for division involves rounding and doubling both the dividend and
divisor. This does not change the solution but can produce
"friendlier" divisors.
Example: 1798 ÷ 52 → 1800 ÷ 50 →
3600 ÷ 100 = 36 (using doubling or 2 as a factor)
Example: 1130 ÷ 24 → 1200 ÷ 25 →
4800 ÷ 100 = 48 (using 4 as a factor)
Example: 1989 ÷ 34 → 2000 ÷ 33 →
2000 ÷ 99 → 2000 ÷ 100 = 20 (Using 3 as a
factor)
Example: 2223.98 ÷ 5 → 2224 ÷ 5 →
4448 ÷ 10 = 445 (Using 2 as a factor)
Why this works: Twice as many people are sharing twice as much, each
still gets the same share.
| In Brief:
Multiplication: the factors change in opposite directions.
Division the dividend and divisor change in the same direction. |
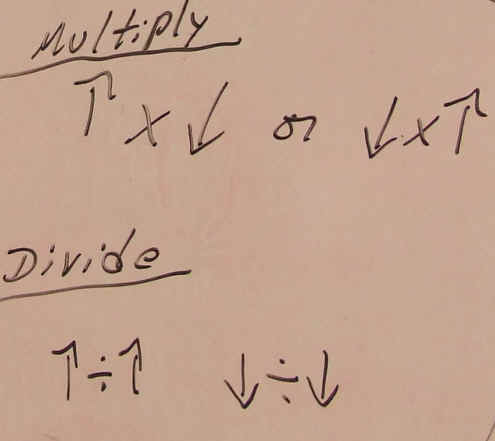 |